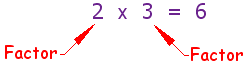This is the third post in my Project Euler series (if series is the right word). The second problem is here.
The prime factors of 13195 are 5, 7, 13 and 29.
What is the largest prime factor of the number 600851475143 ?
This problem seemed rather daunting to me at first. Upon first reading it, I thought to myself ‘I know I’ve learned about prime factors before.’ But unfortunately, somewhere along the lines of learning calculus, linear algebra, and discrete math I forgot about those little prime factor thingys.
So, with a little help from Math is Fun and the ever-present ruler of knowledge Wikipedia, I quickly remembered what prime factors are.
Firstly, what is a factor? When you multiply numbers together, those numbers are called factors. For example (image supplied from Math is Fun):
Simple enough. So a prime factor, obviously, is a factor that is prime. The easiest way to calculate all of the prime factors of a number is divide out all of the 2’s, then the 3’s, and so on. Here’s an example of finding the prime factors of 12.
|
1 2 3 4 5 6 7 8 9 10 |
12 / 2 = 6 #A Whole number, so we divide by 2 again. 6 / 2 = 3 #A Whole number so we divide by 2 again 3 / 2 = 1.5 #Not a whole number so we skip this result and stop dividing out 2's. 3 / 3 = 1, so we're done 2 * 2 * 3 = 12 |
The way this works is quite simple. By dividing out all of the 2’s, we know that we have divided out all of the multiples of 2. If we divided out 4 before 2, then we would be left with a non-prime factor. But by dividing all of the 2’s out of x, we’ll be left with some x’ that is not divisible by any multiples of 2.
This simple, albeit non-efficient method allows us to write an answer quite easily.
Here’s the generic answer, complete with a few optimizations (for example, skipping all multiples of 2). I chose to use longs instead of ints just to make the answer slightly more generic.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
long largestPrimeFactor(long n) { long d = 2; long max = -1; if(n% 2 == 0) //if divisible by 2, divide out all of the 2's { max = 2; do { n/=2; } while(n % 2 == 0); } if(n%3 == 0) //if divisible by 3, divide out all of the 3's { max = 3; do { n/=3; } while(n % 3 == 0); } //Skip to 5, because we know that checking 4 is useless. d = 5; while(n > 1) { //Divide out all d's until n is no longer divisible by d. while (n % d == 0) { if(d > max) { max = d; } n /= d; } d+=2; //skip all evens if(d*d > n) //If d*d is greator than n, then n is not divisible by any d+i. { if(n > 1) { if(n > max) { max = n; } break; } } } return max; } |